用于FSM的三种最受欢迎的编码是二进制(Binary)、格雷(Gray)和独热码(one-hot)。
二进制编码
二进制编码是在将值顺序分配给状态时可以直观使用的简单方法。这样,您将使用尽可能少的位来编码状态。
二进制编码的示例
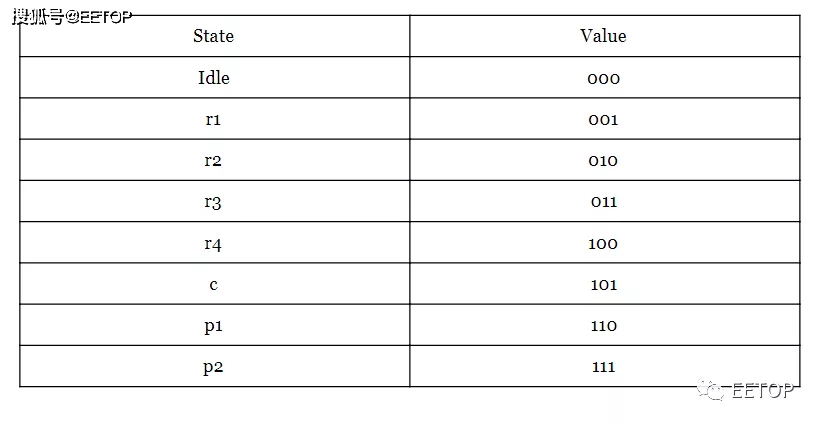
格雷码
在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同,则称这种编码为格雷码(Gray Code),另外由于最大数与最小数之间也仅一位数不同,即“首尾相连”,因此又称循环码或反射码。此外如果状态序列得到最佳遵循,则此编码还可将动态功耗降至最低。
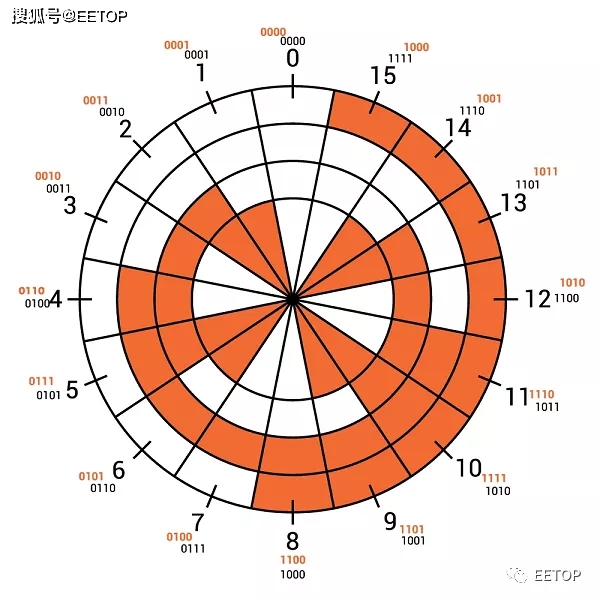 格雷码轮
格雷码轮
独热编码
独热编码任何状态只有1bit为1,其余皆为0,编码密度低,由于使用的位数和无效状态的过多,这似乎不太有效。但是,独热编码非常适合简化触发器的激励逻辑,因为位就是状态,因此无需解码状态。
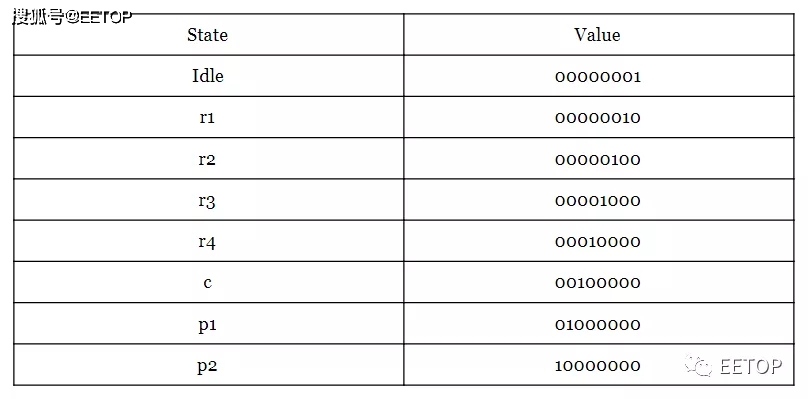
独热编码的示例
这是一个棘手的问题,主要是因为每种编码都有它的优点和缺点,所以它归根结底是一个优化问题,取决于很多因素。
如果一个非常简单的系统在不同的编码中产生非常相似的结果,那么原始编码就是最好的选择。
如果FSM在一条路径上循环地通过其状态(像计数器一样),那么格雷码是一个非常好的选择。
如果FSM有一组任意的状态转换,或者预计在高频下运行,也许独热码是最好的方式。
现在,所有这些说法都只是有根据的猜测,找到最佳状态分配是一个复杂的问题。正因为如此,我建议是让逻辑综合替你决定。尽管如此,下面我决定在三种不同的开发工具和三种不同的状态机对这三种编码的结果进行比较。
接下来的三个实验说明了确定哪种编码适合给定FPGA的过程。
对于此实验,我想大量实例化一个状态机,以放大使用二进制,格雷和独热编码时所得硬件的差异。
我最终选择的系统是康威的《生命的游戏》,这是一种细胞自动机,它模拟了活细胞在其环境中的行为,模拟了这些细胞的出生、繁殖和死亡过程,命游戏是一个二维网格游戏,这个网格中每个方格居住着一个活着或死了的细胞。一个细胞在下一个时刻的生死取决于相邻8个方格中活着或死了的细胞的数量。如果相邻方格活着的细胞数量过多,这个细胞会因为资源匮乏而在下一个时刻死去;相反,如果周围活细胞过少,这个细胞会因为孤单而死去。
在康威的生命游戏中,规定了如下生存定律。
(1)当前细胞为死亡状态时,当周围有3个存活细胞时,则迭代后该细胞变成存活状态(模拟繁殖);若原先为生,则保持不变。
(2)当前细胞为存活状态时,当周围的邻居细胞低于两个(不包含两个)存活时,该细胞变成死亡状态(模拟生命数量稀少)。
(3)当前细胞为存活状态时,当周围有两个或3个存活细胞时,该细胞保持原样。
(4)当前细胞为存活状态时,当周围有3个以上的存活细胞时,该细胞变成死亡状态(模拟生命数量过多)。
这些规则创建了许多有趣的行为和模式,这些行为和模式已在计算机科学中广泛研究。
这就是生命游戏在运行所谓的Gosper滑翔枪时的图例。

《生命游戏》的一种变体,称为Bill Gosper的滑翔机枪。
回到我们的测试系统,每个单元被设计为一个具有8个状态的状态机。不可否认,生命游戏中的细胞逻辑可以在一个周期内解决,但我决定制作一个8状态机,以便在使用不同编码时产生显著差异。这些状态被用来计算一个细胞的存活邻居。
下面一段Verilog代码显示了这些细胞的单元模块结构,包括状态的原始二进制编码。
`define STATE_0 3'b000
`define STATE_1 3'b001
`define STATE_2 3'b010
`define STATE_3 3'b011
`define STATE_4 3'b100
`define STATE_5 3'b101
`define STATE_6 3'b110
`define STATE_7 3'b111
module LifeCell(
inputclk,
inputnrst,
inputseed,
input[7:0] neighbors,
outputreg alive);
reg [2:0] state;
always @ (posedge clk)
if(nrst == 0)
state<= `STATE_0;
else
case(state)
`STATE_0:begin
//...
state<= `STATE_1;
end
`STATE_1:begin
//...
state<= `STATE_2;
end
//...
`STATE_7:begin
//...
state<= `STATE_1;
end
endcase
endmodule
如果您想更深入地了解代码,可以在GitHub上查看该项目。
https://github.com/kuashio/conways-game-of-life
FPGA编码实现
该系统被综合并实现为一个23x23细胞的世界,共有27个变体:使用了三种不同的FSM,都使用了上述三种编码,并且都在三种不同的目标FPGA上实现。
FSM#1:原始模型
该机器有一个初始状态,运行一次,然后循环运行其余7个状态。这几乎是一个完整的序列,所以一开始我觉得格雷编码很有希望。

FSM#2:序列
这台机器表现为3位计数器,所以我也期待格雷编码能碾压竞争对手。

FSM#3:任意路径纠结
该机器具有与FSM#1相同的关键路径,但是当已知存在的邻居数量超过3个时,它将会通过任意路径。
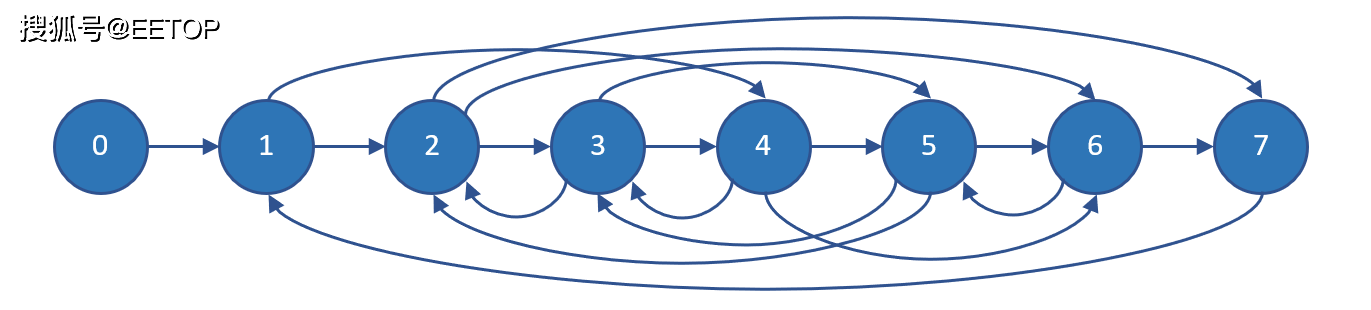
对于这种任意状态转换行为,我希望独热编码是最佳选择。
目标架构
该系统针对三款目标FPGA,利用其供应商的开发工具实现。
结果比较
比较两个或多个系统的性能很困难,主要是因为判决取决于我们使用的指标以及我们认为哪些方面比其他方面更重要。在本实验中,我收集了以下数据以为每个实现产生一个分数:
比较两个或更多系统的性能是很困难的,主要是因为判决取决于我们使用的指标,以及我们认为哪些方面比其他方面更重要。在这个实验中,我收集了以下数据,以便为每个实现打一个分数:
对于每一个实施方案,这四个方面在三个编码之间进行比较,所以在编码之间,我得到一个最好的,一个最差的,一个中间的结果。最好的得正分,最差的得负分,中间的得0分。
将每个模型的所有分数相加后,我得到以下结果:

所有27种实现的结果表。在每一行中,最好的编码用绿色显示,最差的用红色显示,如果没有平局,中间的用黄色显示。
这似乎表明要远离独热编码,只有两种情况下它会获胜,其中一种是平局。此外,虽然我最初认为独热编码是FSM模型#3的最佳编码,但结果却是最差的编码,没有开发工具推荐它。不过在某些情况下,独热编码会胜过其他的,主要是在频率和功率指标上。
总体而言,格雷编码似乎是此特定系统的最佳选择。
从该表中提取赢家,我们得到以下信息:
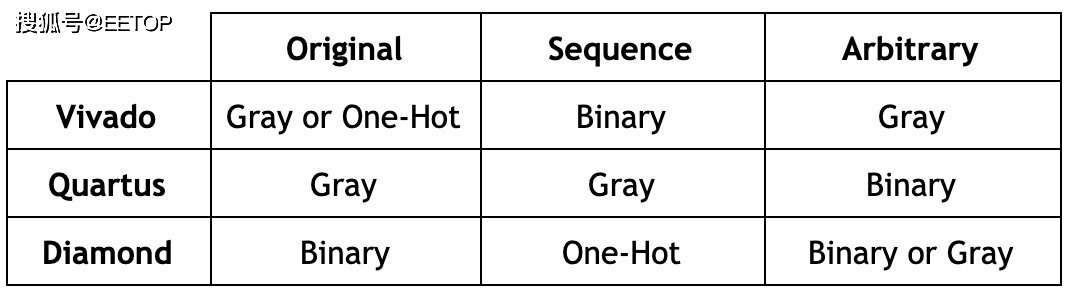
尽管这次比较似乎偏向于格雷编码而不是二进制和独热,但结果在很大程度上取决于我们使用的指标,而这些指标是反映了对我们重要的东西。例如,在这次比较中,我们认为频率和功率比使用率(设计中的逻辑元件和寄存器数量)更重要。如果我重视使用率而不是频率,或重视频率而不是功率,肯定会得出不同的排名。
这个比较并不是为了成为使用这些编码所获得的性能的权威性工作。相反,它显示了我在使用的架构中的个人偏好所产生的排名。
提醒一下,如果你想看看代码,看看27个实现,或者看看我对《生命游戏》的模拟操作,请查看GitHub上的项目:
https://github.com/kuashio/conways-game-of-life